백준[BOJ] 1389번(케빈 베이컨의 6단계 법칙) Python

문제 링크: https://www.acmicpc.net/problem/1389

---

문제 설명

임의의 두 사람이 최소 몇 단계 만에 이어질 수 있는지 계산하는 것이다.
예를 들어 1과 3이 친구이고 1과 4가 친구, 4와 5가 친구, 4와 3이 친구, 3과 2가 친구라고 생각해보자.
그러면 그림은 이와 같이 그려진다.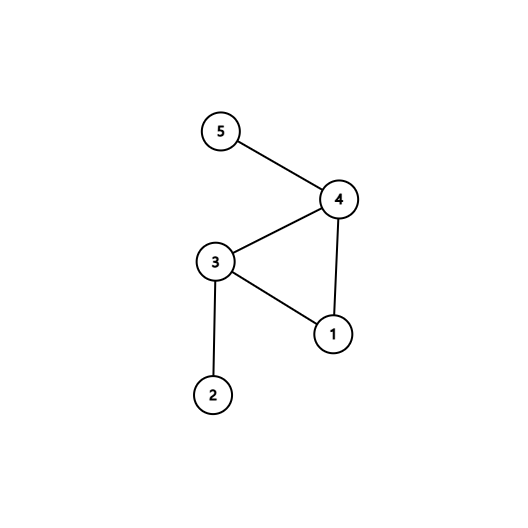

1. 1과 2는 3을 거쳐서 2단계만에 이어진다.
2. 1과 3은 1단계만에 이어진다.
3. 1과 4도 1단계만에 이어진다.
4. 1과 5는 4를 거쳐서 2단계만에 이어진다.
5. 케빈 베이컨의 수는 2+1+1+2=6이다.

같은 방식으로 케빈 베이컨 수를 구하면 2는 8, 3은 5, 4는 5, 5는 8이 나온다. 가장 낮은 케빈 베이컨 수를 가진 유저는 3과 4이다.
여러 명일 경우 숫자가 더 낮은 3이 답이 된다.

---

문제 접근

위의 사진처럼 정점과 간선으로 이루어진 그래프라고 생각하면 결국 최단거리를 구하는 것과 마찬가지이므로 BFS를 이용해야겠다고 생각했다. 기본 BFS문제와 비슷해보여서 나름 쉽게 풀었다. 큐를 이용해 현재 정점을 큐에 넣고 방문처리해준다. 더 이상 방문한 정점이 없을 때까지(큐가 빌 때까지) 반복해준다. 큐에 넣은 현재 정점은 방문처리 되었으므로 pop 해주고 현재 정점의 인접한 정점을 찾아서 큐에 넣어주고 그 인접한 정점들에 대해서 탐색하며 방문처리를 해준다.
방문 처리 할 때마다 count를 해주어 단계를 증가시켜주었다.

---

Python code

from collections import deque

def dfs(n):
    queue=deque()   #큐에 넣어야하므로 deque 자료구조 사용
    visited[n]=1  #방문처리하고
    queue.append(n)  #큐에 넣어줌
    sum=0   #케빈 베이컨 수를 구하기 위한 변수
    while queue:  #queue가 빌 때까지 반복
        q=queue.popleft()   #pop해주고 그 값을 저장
        for i in graph[q]:  #pop해준 노드와 인접한 노드 확인
            if not visited[i]:  #방문하지 않았다면
                queue.append(i)  #큐에 넣어주고
                visited[i]=visited[q]+1 #단계를 증가시켜줌
        for k in range(len(visited)):  #순회하면서
            if k==n:   #같을 때는 카운트 안하므로 
                continue   #continue해주고
            sum+=visited[k]   #각 단계를 더해줌
        return sum


n,m=map(int, input().split())
graph=[[]for _ in range(n+1)]   #각 노드에 인접한 노드를 저장하는 이차원 리스트
for i in range(m):
    a,b=map(int, input().split())
    graph[a].append(b)
    graph[b].append(a)

result=[]   #케빈 베이컨 수를 저장하는 리스트
for j in range(1, n+1):
    visited=[0]*(n+1)   #한 번 할 때마다 초기화 해줘야함
    result.append(bfs(j))   #각 시작 정점에 대해 케빈 베이컨 수를 저장

x=min(result)
print(result.index(x)+1)